

* When graphing, it is also helpful to find the x-intercepts (the x-value when y=0 : in this case) and y-intercepts (y-value when x=0: in this case) but in this assignment, we focus on the behavior of the graph in terms of the domain, asymptotes or holes, and range. When ad-bc=0, the equation becomes y= (a horizontal line), but is not defined at x= thus, is a horizontal line with a hole at. The graph is symmetric about (p, q) and the asymptotes are x= and y=. When, it is easy to see that the graph of is translated units horizontally and units vertically. So, comparing this equation with the form of discussed above, you can see that !

What affects to the function do you think the parameters a, b, c, and d have?Īny ideas? To find out, we rewrite the equation in a familiar form. Well, we are going to use these mathematical ideas to observe the rational function. What was the observation above all about? When k=0, the equation becomes y=q, but is not defined at x=p thus, is a horizontal line with a hole at (p, q). The graph is symmetric about (p, q) and the asymptotes are x=p and y=q. You may notice that the domain is and range is. When, it is easy to see that the graph of is translated p units horizontally and q units vertically. However, to be defined, note that x cannot be equal to zero and hence there is a hole in the graph at (0, 0). When k<0, the graph is in the second and fourth quadrant.įor k=0, the equation becomes y=0, which is the x-axis. Well, you can see that the larger |k| is, the farther it is from the origin.Īlso, when k>0, the graph is in the first and third quadrant.
The graph is still a hyperbolic curve that is symmetric about the origin and the asymptotes are the same. Well, let’s try a few values for k and see what the graph looks like.įor, both the domain and range do not change.

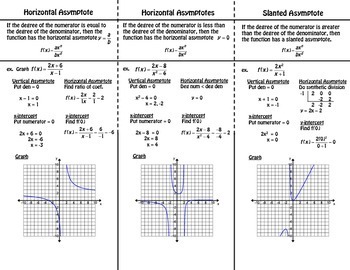
The asymptotes (which are lines that the graph of the function approaches but never touches) are x=0 (the y-axis) and y=0 (the x-axis).Ģ) What changes are there in compared to ? The domain and range are both and the graph is a hyperbolic curve symmetric about the origin, positioned in the first and third quadrants. It is a rational function and it is easy to see that the graph would look like this: What is the domain and range of the function? What does the graph look like? The function is defined when and hence the domain of f is the set of all points x for which. And those are the two asymptotes for this function, it's got an oblique as to y=x-1 slanted like this and a vertical asymptote and that'll be important when you're graphing functions where the degree of the numerator is bigger than the degree of denominator.A rational function has an equation of the form where p(x) and q(x) are polynomials. Now if you, you can either fi- find the vertical asymptotes in the beginning or you can do it now because you're always going to have this denominator here x+2=0 when x is -2 so x=-2 is going to be your vertical asymptote. This is going to be my oblique asymptote right here the x-1 so y=x-1 is an oblique asymptote.
#RATIONAL FUNCTION GRAPH PLUS#
What that means is that f of x is actually equal to this quotient x-1 plus this remainder -2 over this divisor x+2. We have x squared plus x minus 4 divided by x+2 and so what do we need to multiply by x to get x squared, x, so you multiply through and we get x squared plus 2x we change the signs and add and we get –x-4, now what do we need to multiply by x to get minus x, -1, so we multiply -1 through and we get -1,-x-2 change the signs and add and I get a reminder of -2. Now the first thing you want to do is in order to find the oblique asymptote if there is one is divide these two so let's do that. Here I have f of x equals x squared plus x minus 4 over x plus 2 and I want to find the asymptotes. If n is greater than m remember that there are no horizontal asymptotes but there maybe something called an oblique asymptote and the way to find out is to divide the the top polynomial by the bottom polynomial. I want to talk about rational functions where the degree of the numerator is bigger than the degree of the denominator, so remember the rational function is a ratio of two polynomials so let's call the degree of the top polynomial n and the bottom one m.


 0 kommentar(er)
0 kommentar(er)
